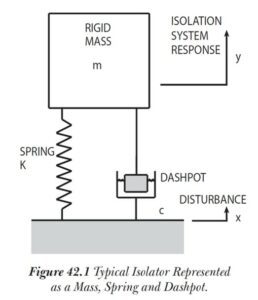
For analysis it is customary to idealize structures, objects and isolation systems as simple mass-spring-damper systems as shown in Figure 42.1. The mass m is infinitely rigid. The spring is weightless and its stiffness is K lbs/in. The damper, or dashpot, is weightless and its damping coefficient is c lbs/in./sec.

Natural Frequency

All objects vibrate when subjected to impact, noise or vibration. When the stimulation is removed, the object will experience periodic sinusoidal oscillations or free vibration at a frequency which is called its Natural Frequency f _n in (Hz cycles/sec). With little or no damping, the Natural Frequency of a simple system such as Figure 42.1 is defined as follows:

f _n = 3.13 (K/W) ^1/2      (1)

Where mass m = W/g, and

     g = acceleration of gravity = 386 in/sec ²

Damping

In a simple system, Damping serves as an energy dissipation “dashpot” to limit the magnification of system response. Actual Damping c is conveniently referenced to
Critical Damping c _c which is the value of damping at which a system will not oscillate when disturbed from equilibrium. Critical Damping is related to the system mass and natural frequency, as follows:

c _c = 78.96 (mf _n ² )     (2)

Forced Vibration, Transmissibility and Resonance

If the simple system in Figure 42.1 is subjected to Forced Vibration at frequency f , and sinusoidal foundation motion at amplitude x , the absolute value of the mass response amplitude y expressed as a ratio |y/x| , also known as Transmissibility T , will be as follows:

   (3)    

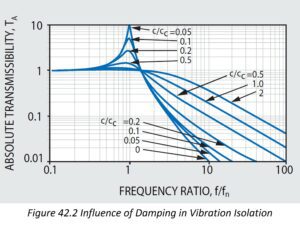
Figure 42.2 is plotted as a function of forcing frequency ratio f/f _n and critical damping ratio c/c _c . If external vibration is applied at a frequency which coincides with the Natural Frequency; i.e., (f/f _n )= 1 , a condition of Resonance occurs. At resonance the system will experience very large potentially damaging magnification of the disturbing forces.

The maximum Transmissibility T _max at resonance is commonly referred to as the Q of the system and is approximately related to Critical Damping, as follows:

T _max = Q = 1/2 c _c     (4)

Dashpot or damping force is proportional to velocity. The forces due to high damping are desirable at resonance to oppose damaging magnification, but less desirable at high frequencies because this tends to negate vibration attenuation. This is evident in Equation (3).

Isolation Efficiency

Isolation Efficiency E in percent transmission is related to Transmissibility as:

E = 100 (1-T)%     (5)

and is the percentage of the vibration isolated from the payload. It should be observed in Equation (3) and Figure 42.2, that in order to achieve the best isolation efficiency the isolator’s natural frequency should be very low. This is the basic philosophy of VIBRAPLANE Isolation.

Center of Gravity (cg)

The Center of Gravity is the point in an object where an external applied force produces displacement but no rotation. Typically the center of gravity will be located near the largest concentration of mass in the object and may be located by computation or experimental means. Equipment cg height and geometry are very important for considerations of stability and rocking when using soft supports to achieve vibration isolation. For best stable results, KSI recommends the cg height should not exceed 25% of the shortest span between supports.

Air Spring Stiffness and Natural Frequency

VIBRAPLANE isolation systems utilize the properties of compressed air to provide the uniquely low stiffness properties essential for the high efficiency broad frequency band isolation essential for high technology equipment. The Air Spring Stiffness K in lbs/in. is a function of absolute pressure P in psi, area A in sq. in., and volume V in cu. in., as follows:

K = PA ² / V     (6)

Combining Equations (1) and (6), the simple Air System Natural Frequency is:

f _A = 3.13 (A / V) ^1/2      (7)

It is basic to note in Equation (7) that increasing the air volume of the air spring results in a lower system natural frequency which is necessary for high isolation efficiently.